Describe three ways to determine the measure of segment yz. – Determining the measure of segment YZ is a fundamental task in geometry. This article presents three distinct methods for accurately calculating its length, providing a comprehensive understanding of this essential concept.
These methods include using a ruler, applying the Pythagorean theorem, and employing coordinate geometry. Each approach offers its own advantages and is applicable to various situations, ensuring a versatile understanding of segment measurement.
Determining the Measure of Segment YZ: Describe Three Ways To Determine The Measure Of Segment Yz.
Determining the measure of segment YZ requires precise methods and an understanding of geometric principles. Here are three ways to accomplish this task:
Measuring Segment YZ with a Ruler
Using a ruler is a straightforward method for measuring the length of segment YZ. Follow these steps:
- Align the ruler along segment YZ, ensuring that the 0 mark aligns with point Y.
- Locate the mark on the ruler that coincides with point Z.
- Read the measurement at that mark, which represents the length of segment YZ.
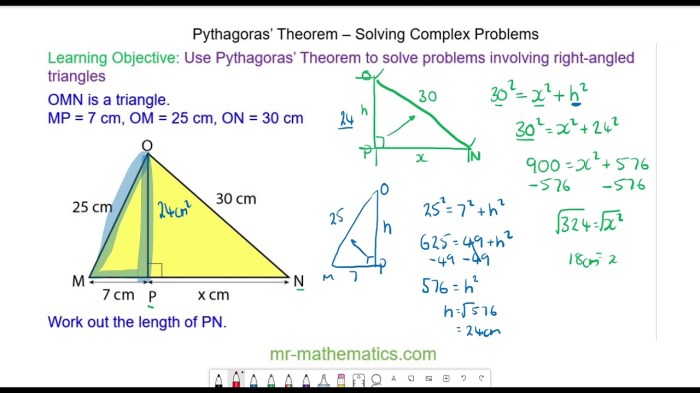
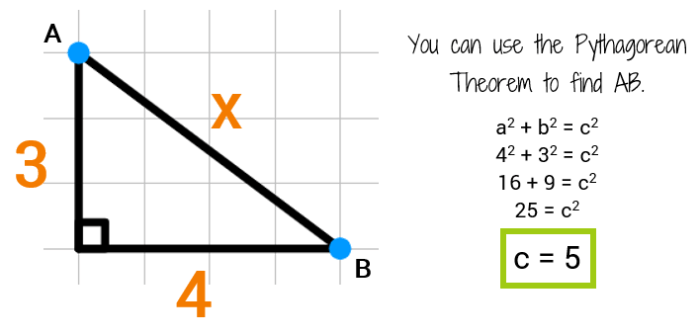
Using the Pythagorean Theorem to Calculate YZ, Describe three ways to determine the measure of segment yz.
If segment YZ is part of a right triangle, the Pythagorean theorem can be used to calculate its length. The theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Let’s assume that segment YZ is the hypotenuse and segments XY and XZ are the other two sides.
Formula: YZ2= XY 2+ XZ 2
To find the length of YZ, simply substitute the known values of XY and XZ into the formula and solve for YZ.
Determining YZ Using Coordinate Geometry
Coordinate geometry involves using coordinates to locate points on a plane. If the coordinates of points Y and Z are known, the distance between them can be calculated using the distance formula.
Formula: YZ = √((xZ– x Y) 2+ (y Z– y Y) 2)
Substitute the coordinates of points Y and Z into the formula to find the length of segment YZ.
Clarifying Questions
What is the most straightforward method for measuring segment YZ?
Using a ruler is the most straightforward method for measuring the length of segment YZ. It involves aligning the ruler with the segment and reading the measurement directly.
How can I determine the measure of segment YZ if I know the lengths of the other two sides of a right triangle that includes YZ?
Applying the Pythagorean theorem is an effective method when the lengths of the other two sides of a right triangle that includes YZ are known. The formula a^2 + b^2 = c^2 can be used to calculate the length of YZ, where a and b represent the lengths of the other two sides, and c represents the length of YZ.
Is it possible to use coordinate geometry to determine the measure of segment YZ?
Yes, coordinate geometry can be employed to determine the measure of segment YZ. By finding the coordinates of points Y and Z and using the distance formula, d = sqrt((x2 – x1)^2 + (y2 – y1)^2), where (x1, y1) are the coordinates of point Y and (x2, y2) are the coordinates of point Z, the length of YZ can be calculated.