Distance From Point A To Point B

Distance from point a to point b – The distance between two points is a fundamental concept in geometry and has wide-ranging applications in various fields. From navigation systems to scientific research, understanding how to calculate distance is essential for accurate measurements and effective planning.

This article delves into the mathematical definitions, methods, and applications of distance calculation. It explores the factors that can affect distance measurements and provides practical examples to illustrate the concepts discussed.

Defining the concept of distance

Distance is a fundamental concept in mathematics and physics, referring to the measure of the separation between two points or objects. It plays a crucial role in various fields, including geometry, navigation, and engineering.

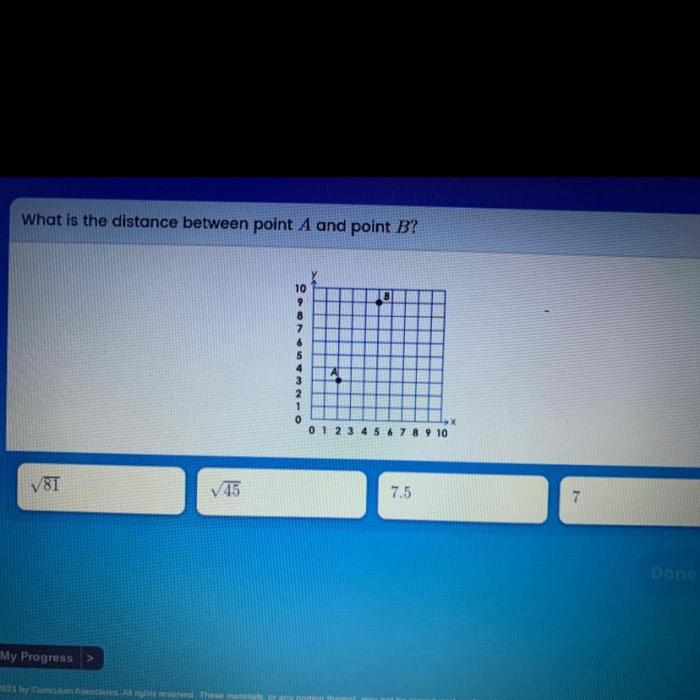
Mathematically, the distance between two points, denoted as A and B, is defined as the length of the line segment connecting them. In Euclidean geometry, this distance is calculated using the Euclidean distance formula:

d = √((x₂

x ₁) ²+ (y ₂

y ₁) ²)

where (x ₁, y ₁) and (x ₂, y ₂) are the coordinates of points A and B, respectively.

Units of measurement

Distance can be measured in various units, including:

Metric system:meters (m), kilometers (km)
Imperial system:feet (ft), miles (mi)
Nautical miles:used in navigation
Astronomical units:used in astronomy

Applications

Distance calculations have numerous applications, such as:

Determining the distance between two cities or countries
Calculating the length of a road or river
Estimating the distance traveled by a vehicle or spacecraft
Determining the radius of a circle or sphere

Methods for calculating distance: Distance From Point A To Point B

Determining the distance between two points is a fundamental concept in geometry and various other fields. Several methods exist to calculate distance, each with its own advantages and applications.

Pythagorean Theorem

The Pythagorean theorem is a fundamental theorem in geometry that relates the lengths of the sides of a right triangle. It states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

$a^2 + b^2 = c^2$

Where:

$a$ is the length of one leg of the right triangle
$b$ is the length of the other leg of the right triangle
$c$ is the length of the hypotenuse

The Pythagorean theorem can be used to calculate the distance between two points on a plane by forming a right triangle with the two points as the endpoints of the legs and the distance between them as the hypotenuse.

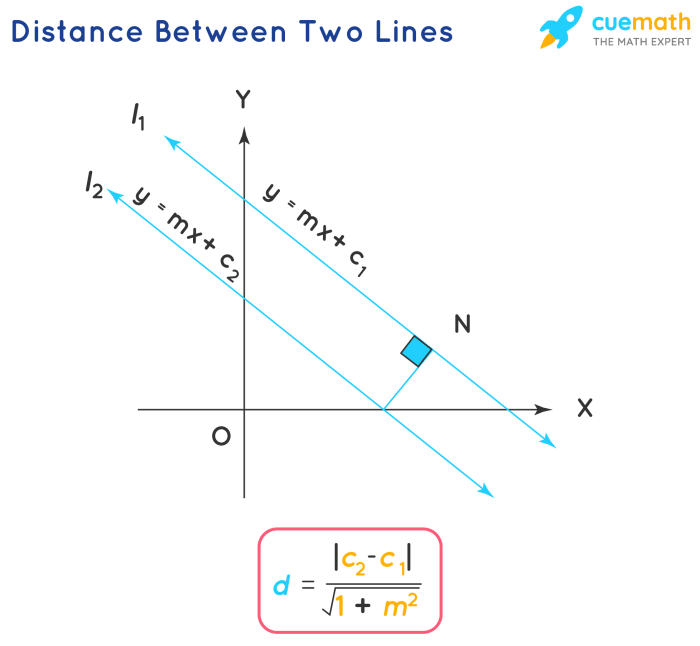
Distance Formulas

Distance formulas provide a direct method for calculating the distance between two points. The most common distance formula is the Euclidean distance formula, which calculates the distance between two points in a Euclidean space.

$d = \sqrt(x_1

x_2)^2 + (y_1

y_2)^2$

Where:

$d$ is the distance between the two points
$(x_1, y_1)$ are the coordinates of the first point
$(x_2, y_2)$ are the coordinates of the second point

The Euclidean distance formula can be extended to higher dimensions to calculate distances in three-dimensional space or even higher.

Shortest Path Algorithms

Shortest path algorithms are used to find the shortest path between two points in a graph or network. These algorithms take into account the weights or distances associated with the edges of the graph and find the path with the minimum total weight or distance.

Some common shortest path algorithms include:

Dijkstra’s algorithm
Bellman-Ford algorithm
A* search algorithm

Shortest path algorithms have applications in various fields, such as routing in computer networks, finding the shortest route on a map, and optimizing transportation systems.

Applications of distance calculation

The concept of distance finds extensive applications in various domains, including navigation, logistics, and scientific research.

In navigation systems, such as GPS (Global Positioning System), distance plays a crucial role in determining the position of a receiver. GPS satellites transmit signals containing their precise location and time information. By measuring the time difference between receiving signals from multiple satellites, the receiver can calculate its distance from each satellite.

Using triangulation, the receiver can then determine its own position.

Logistics and Transportation Planning

In logistics and transportation planning, distance is a key factor in optimizing routes and schedules. By calculating the distance between different locations, logistics companies can determine the most efficient routes for transporting goods. This helps in reducing transportation costs, improving delivery times, and enhancing overall supply chain efficiency.

Scientific Research

Distance is also a fundamental concept in scientific research, particularly in fields such as astronomy and physics. In astronomy, distance measurements are crucial for determining the size, structure, and evolution of celestial objects. For instance, astronomers use parallax methods to measure the distance to nearby stars by observing their apparent shift in position as the Earth orbits the Sun.

Factors affecting distance measurement

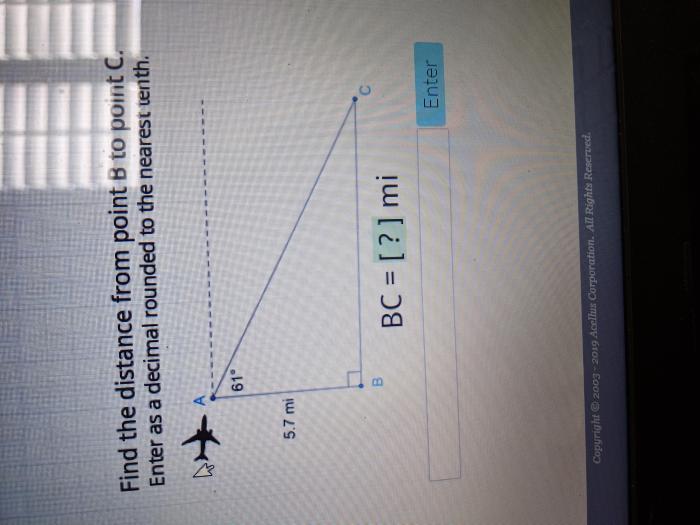
The accuracy of distance measurements can be affected by several factors, including measurement errors and environmental conditions. Measurement errors can arise from various sources, such as instrument calibration, human error, and environmental interference. Environmental conditions, such as temperature, humidity, and atmospheric pressure, can also influence the accuracy of distance measurements by affecting the propagation of electromagnetic waves or sound waves used in distance measurement techniques.

Impact of different coordinate systems on distance calculations

Distance calculations are also affected by the choice of coordinate system used. Different coordinate systems, such as Cartesian coordinates, polar coordinates, and spherical coordinates, represent positions in different ways. The choice of coordinate system can impact the distance calculations, as the distance between two points may vary depending on the coordinate system used.

Concept of error propagation in distance measurements, Distance from point a to point b

Error propagation is a concept that describes how errors in measurements propagate through calculations. In distance measurements, errors in the measurement of individual distances can propagate through subsequent calculations, leading to an accumulation of errors in the final result. Understanding error propagation is important for assessing the accuracy and reliability of distance measurements.

Visualizing distance using tables

Tables provide a structured and organized way to present data related to distance measurements. They allow for easy comparison and analysis of distances, units, and other relevant information.

Creating an HTML table for distance measurements

To create an HTML table for distance measurements, use the following steps:

Start by creating a table element using the
tag.

Define the table header using the

tag and the table body using the

tag.

Within the table header, create table headings using the

tag and table data cells using the

tag for each column, such as “Distance,” “Units,” and any additional information.

Within the table body, create table rows using the

tag for each piece of data.

Format the table using CSS to ensure it is responsive and easy to read on different devices.

Here is an example of an HTML table for distance measurements:

“`html

Distance	Units	Additional Information
100	kilometers	Distance from City A to City B
50	miles	Distance from Town X to Town Y

“`

FAQ Overview

What is the mathematical definition of distance between two points?

The distance between two points in a Euclidean space is the length of the line segment connecting them.

What are the common units of measurement for distance?

The most common units of measurement for distance are meters, kilometers, miles, and feet.

How is distance used in navigation systems?

Navigation systems use distance measurements to calculate the shortest path between two points and provide directions to the user.